Pierre de Fermat
René Descartes
One of the greatest achievements in the development of mathematics since Euclid was the introduction of coordinates. Two men take credit for this development: Fermat and Descartes (Renatus Cartesius).
These two great French mathematicians were interested in the unification of geometry and algebra, which resulted in the creation of a most fruitful branch of mathematics now called analytic geometry. Fermat and Descartes who were heavily involved in physics, were keenly aware of both the need for quantitative methods and the capacity of algebra to deliver that method.

Fermat’s interest in the unification of geometry and algebra arose because of his involvement in optics. His interest in the attainment of maxima and minima—thus his contribution to calculus—stemmed from the investigation of the passage of light rays through media of different indices of refraction, which resulted in Fermat’s principle in optics and the law of refraction. With the introduction of coordinates, Fermat was able to quantify the study of optics and set a trend to which all physicists of posterity would adhere. It is safe to say that without analytic geometry the progress of science, and in particular physics, would have been next to impossible.

Born into a family of tradespeople, Pierre de Fermat (1607--1665)was trained as a lawyer and made his living in this profession becoming a councilor of the parliament of the city of Toulouse. Although mathematics was but a hobby for him and he could devote only spare time to it, he made great contributions to number theory, to calculus, and, together with Pascal, initiated work on probability theory.

The coordinate system introduced by Fermat was not a convenient one. For one thing, the coordinate axes were not at right angles to one another. Furthermore, the use of negative coordinates was not considered.

René Descartes (1596--1650) was a great philosopher, a founder of modern biology, and a superb physicist and mathematician. His interest in mathematics stemmed from his desire to understand nature. His father, a relatively wealthy lawyer, sent him to a Jesuit school at the age of eight where, due to his delicate health, he was allowed to spend the mornings in bed, during which time he worked. He followed this habit during his entire life. At twenty he graduated from the University of Poitier as a lawyer and went to Paris where he studied mathematics with a Jesuit priest. After one year he decided to join the army of Prince Maurice of Orange in 1617. During the next nine years he vacillated between various armies while studying mathematics.

René eventually returned to Paris, where he devoted his efforts to the study of optical instruments motivated by the newly discovered power of the telescope. In 1628 he moved to Holland to a quieter and freer intellectual environment. There he lived for the next twenty years and wrote his famous works. In 1649 Queen Christina of Sweden persuaded Descartes to go to Stockholm as her private tutor. However the Queen had an uncompromising desire to draw curves and tangents at 5 a.m., causing Descartes to break the lifelong habit of getting up at 11 o’clock! After only a few months in the cold northern climate, walking to the palace for the 5 o’clock appointment with the queen, he died of pneumonia in 1650.

Throughout the seventeenth century, mathematicians used one axis with the y values drawn at an oblique or right angle onto that axis. Newton, however, in a book called "The Method of Fluxions and Infinite Series" written in 1671, and translated much later into English in 1736, describes a coordinate system in which points are located in reference to a fixed point and a fixed line through that point. This was the first introduction of essentially the polar coordinates we use today.

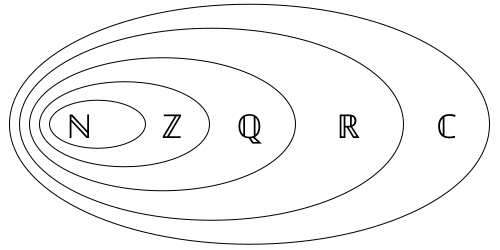
Coordinate Systems

Most likely, you are more comfortable working with the vector spaces ℝn or ℂn and their subspaces than with other types of vectors spaces and subspaces. The objective of this section is to impose coordinate systems on arbitrary vector space even if it is not your lovely 𝔽n. In this section, you will learn that for finite dimensional vector spaces, no loss of generality results from restricing yourself to the space 𝔽n.

Ordered Bases

The vector [2, 3, −1] in ℝ³ can be expressed in terms of the standard basis vectors as 2e₁ + 3e₂ − e₃ or, in more familiar form as 2i + 3j − k. The components of [2, 3, −1] are precisely the coeficients of these basis vectors. The vector [2, 3, −1] is different from the vector [3, 2, −1] just as the point (2, 3, −1) is different frm the point (3, 2, −1). We regard the standard basis vectors as havng natural order e₁ = [1, 0, 0] = i, e₂ = [0, 1, 0] = j and e₃ = [0, 0, 1] = k. In nonzero vector space V with basis β = {b₁, e₂, … , en}, there is usually no natural order for the basic vectors. When order does not matter, mathematicians embrace a set in curly brackets. For example, vectors {j, i, k} also form a basis in ℝ³ (called the left-handed). If we want the vectors to be displayed in some order, we must specify their order. For eample, there are 3! = 6 possible ordered presentations of basic vectors:
\[ \begin{array}{ccc} {\bf ijk} & {\bf jik} & {\bf jki} \\ {\bf ikj} & {\bf kij} & {\bf jki} \end{array} \]
Mathematica confirms:
Permutations[{i, j, k}]
{{i, j, k}, {i, k, j}, {j, i, k}, {j, k, i}, {k, i, j}, {k, j, i}}
By convention, set notation with curly brackets indicates that there is no order within the set. If we want basic vectors to be labeled or displayed with some order, we place them within either parentheses or brackets---both notations work. Hencs, we denote an ordered basis of n vectors of V by β = [b₁, b₁, … , bn]. n

Coordinatization

Let V be a finite dimensional vector space over field 𝔽, and let β = [b₁, b₂, … , bn] be an ordered basis for V. We know from section that every vector x in V can be expressed in the form
\begin{equation} \label{EqCoord.1} {\bf x} = x_1 {\bf b}_1 + x_2 {\bf b}_2 + \cdots + x_n {\bf b}_n \end{equation}
for unique scalars x₁, x₂, … , xn. For comleteness of our exposition, we formulate this fact as theorem.

Theorem 1: Let V be a vector space over field 𝔽 and let β = {b1, b2, … . bn} be a basis of V. For every vector x in V, there exists a unique set of scalars c1, c2, … , cn such that Eq.(1) holds.

Let β be a basis for V. If \( {\bf v} \in V , \) then v belongs to the span of the basis β. Then there exist scalars c1, c2, … , cn such that \[ {\bf v} = c_1 {\bf v}_1 + c_2 {\bf v}_2 + \cdots + c_n {\bf v}_n . \] Suppose that we could also write another expansion \[ {\bf v} = d_1 {\bf v}_1 + d_2 {\bf v}_2 + \cdots + d_n {\bf v}_n . \] Subtract these two equations and obtain \[ {\bf 0} = \left( c_1 - d_1 \right) {\bf v}_1 + \left( c_2 - d_2 \right) {\bf v}_2 + \cdots + \left( c_n - d_n \right) {\bf v}_n . \] However, a basis is a linearly independent set, so it follows that each coefficient of this equation is zero, whence c1 = d1, c2 = d2 , … , cn = dn.
The converse of Theorem 1 is also true. That is, if β is a set of vectors in a vector space V with the property that every vector in V can be written uniquely as a linear combination of the vectors in β, then β is a basis for V. In this sense, the unique representation property characterizes a basis. In view of this fact, we may speak of coordinates of a vector relative to a basis. Here is the notation that we employ:
Suppose that β = {b1, b2, … . bn} is an ordered basis for a vector space V and x is in V. The coordinates of x relative to the basis β (or β-coordinates of x) are the weights x₁, x₂, … , xn such as \[ {\bf x} = x_1 {\bf b}_1 + x_2 {\bf b}_2 + \cdots + x_n {\bf b}_n . \tag{1} \] The vector with entries x₁, x₂, … , xn is called the coordinate vector of x relative to (or with respect to) β and it is denoted by [x]β = (x₁, x₂, … , xn). Each xi (∀i) is named component of the coordinate vector [x]β.

Note that by definition, a basis of a vector space is a set of vectors that generate the space. In order to use a basis for coordinate system, we need to order the basis and consider it as a list of vectors. Then coordinates of the vector follow the prescribed order of basis vectors. Otherwise, the summands in Eq.(1) can be reordered without altering the final answer---summation of vectors is commutative.


A coordinate vector [x]β can be written as a vector column (∈ 𝔽n×1), or vector row (∈ 𝔽1×n), or as an n-tuple (∈ 𝔽n). When matrix multiplication is involved, column notation is preferable for using coordinate vectors.

Example 1: In vector space of polynomials ℝ≤2[x], consider ordered set β = {x − x², 2 + x. 3 + x²} of linearly independent polynomials.

First, we verify that polynomials from the set β are linearly independent. Let c₁, c₂, c₃ be scalars such that \[ c_1 \left( x - x^2 \right) + c_2 \left( 2 + x \right) + c_3 \left( 3 + x^2 \right) = 0 . \] Then \[ \left( 2\,c_2 + 3\, c_3 \right) + \left( c_1 + c_2 \right) x + \left( -c_1 + c_3 \right) x^2 = 0 . \] This implies that \[ \begin{split} 2\,c_2 + 3\, c_3 &= 0 , \\ c_1 + c_2 &= 0 , \\ -c_1 + c_3 &= 0, \end{split} \] the solution to which is c₁ = c₂ = c₃ = 0 because the matrix of the system \[ \begin{bmatrix} 0 & 2 & 3 \\ 1 & 1 & 0 \\ -1 & 0 & 1 \end{bmatrix} \] is invertible (its determinant is 1). Hence, polynomials in set β are linearly independent and the set is basis for ℝ≤2[x].

Since set β is basis, we can expand any polynomial of degree at most 2 into linear combination of polynomials from β. For example, \[ \left( 1 + x \right)^2 = c_1 \left( x - x^2 \right) + c_2 \left( 2 + x \right) + c_3 \left( 3 + x^2 \right) . \] This relation is valid when \[ \begin{split} 1 &= 2\,c_2 + 3\, c_3 , \\ 2 &= c_1 + c_2 , \\ 1 &= -c_1 + c_3 . \end{split} \] Mathematica easily solve this system of equations

Solve[{1 == 2 c2 + 3 c3, 2 == c1 + c2 , 1 == -c1 + c3}, {c1, c2, c3}]
{{c1 -> -6, c2 -> 8, c3 -> -5}}
So we get \[ \left( 1 + x \right)^2 = 1 + 2\,x + x^2 = -6 \left( x - x^2 \right) + 8 \left( 2 + x \right) -5 \left( 3 + x^2 \right) . \]
End of Example 1
■
Example 2: The following vectors form a basis β of ℝ³: b₁ = (1, 2, 3), b₂ = (1, −1, 2), b₃ = (3, 2, −1). We check their linearly independence with Mathenatica:
Det[{{1,2,3}, {1,-1,2}, {3,2,-1}}]
26
Since the determinant of the matrix A = [b₁ b₂ b₃ ] built from these three vectors is not zero, the given vectors are linearly independent. As we know the dimension of ℝ³ to be 3, these three vectors form a basis.

Let us find the coordinate vector of v = (8, 1, −7) with respect to this basis written as a list of the given three vectors β = {b₁, b₂, b₃}. So we need to find scalars c₁, c₂, c₃ such that \[ {\bf v} = c_1 {\bf b}_1 + c_2 {\bf b}_2 + c_3 {\bf b}_3 . \] Writing vectors in column form, we obtain \[ \begin{bmatrix} \phantom{-}8 \\ \phantom{-}1 \\ -7 \end{bmatrix} = c_1 \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + c_2 \begin{bmatrix} \phantom{-}1 \\ -1 \\ \phantom{-}2 \end{bmatrix} + c_3 \begin{bmatrix} \phantom{-}3 \\ \phantom{-}2 \\ -1 \end{bmatrix} , \] which we can rewrite in matrix form \[ \begin{bmatrix} \phantom{-}8 \\ \phantom{-}1 \\ -7 \end{bmatrix} = \begin{bmatrix} 1&\phantom{-}1&\phantom{-}3 \\ 2&-1&\phantom{-}2 \\ 3&\phantom{-}2& -1 \end{bmatrix} \,\begin{bmatrix} c_2 \\ c_2 \\ c_3 \end{bmatrix} , \qquad \mbox{with} \quad {\bf A} = \left[ {\bf b}_1 \ {\bf b}_2 \ {\bf b}_3 \right] = \begin{bmatrix} 1&\phantom{-}1&\phantom{-}3 \\ 2&-1&\phantom{-}2 \\ 3&\phantom{-}2& -1 \end{bmatrix} . \] This allows us to rewrite the linear system in compact form: \[ {\bf A}\, {\bf c} = {\bf k}, \qquad \mbox{where} \quad {\bf c} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix} , \quad {\bf k} = \begin{bmatrix} \phantom{-}8 \\ \phantom{-}1 \\ -7 \end{bmatrix} . \] With the aid of Mathematica, we find the inverse matrix and apply it to the vector k:

B = Inverse[{{1, 1, 3}, {2, -1, 2}, {3, 2, -1}}]
{{-(3/26), 7/26, 5/26}, {4/13, -(5/13), 2/13}, {7/26, 1/26, -(3/26)}}
\[ {\bf A}^{-1} = \begin{bmatrix} 1&\phantom{-}1&\phantom{-}3 \\ 2&-1&\phantom{-}2 \\ 3&\phantom{-}2& -1 \end{bmatrix}^{-1} = \frac{1}{26} \begin{bmatrix} -3&7&5 \\ 8& -10 & 4 \\ 7 & 1 & -3 \end{bmatrix} . \] So
B . {8, 1, -7}
{-2, 1, 3}
\[ {\bf c} = {\bf A}^{-1} {\bf k} = \frac{1}{26} \begin{bmatrix} -3&7&5 \\ 8& -10 & 4 \\ 7 & 1 & -3 \end{bmatrix} \begin{bmatrix} \phantom{-}8 \\ \phantom{-}1 \\ -7 \end{bmatrix} = \begin{bmatrix} -2 \\ 1 \\ 3 \end{bmatrix} . \] This shows us that \[ {\bf v} = \begin{bmatrix} \phantom{-}8 \\ \phantom{-}1 \\ -7 \end{bmatrix} = (-2) \,{\bf b}_1 + {\bf b}_2 + 3\,{\bf b}_3 = (-2) \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} + \begin{bmatrix} \phantom{-}1 \\ -1 \\ \phantom{-}2 \end{bmatrix} + 3 \begin{bmatrix} \phantom{-}3 \\ \phantom{-}2 \\ -1 \end{bmatrix} . \] We have shown that the coordinate vector of v with respect to basis β is [v]β = (−2, 1, 3).
End of Example 2
■

Coordinate vectors are strictly related to a basis imposed in a vector space. Any finite dimensional vector space is isomorphic to 𝔽n, and any chosen basis establishes such bijection to 𝔽n, where 𝔽 is a field of the given vector space. In some cases, we need to verify that vectors { b1, b2, … , bn } form a basis in ℝn (we mostly use real numbers as a field). In other words, we need to verify that these vectors are linearly independent, which is equivalent to condition that the system A x = 0 has only trivial solution, where A = [b1, b2, … , bn]. This in turn is equivalent to the matrix A being of full column rank n or being invertible.

=========================== to be checked

  If the vectors \( \left\{ {\bf u}_1 , {\bf u}_2 , \ldots , {\bf u}_n \right\} \) form a basis for a vector space V, then every vector in V can be uniquely expressed in the form

\[ {\bf v} = \alpha_1 {\bf u}_1 + \alpha_2 {\bf u}_2 + \cdots + \alpha_n {\bf u}_n \]
for appropriately chosen scalars \( \alpha_1 , \alpha_2 , \ldots , \alpha_n . \) Therefore, v determines a unique n-tuple of scalars \( \left[ \alpha_1 , \alpha_2 , \ldots , \alpha_n \right] \) and, conversely, each n-tuple of scalars determines a unique vector \( {\bf v} \in V \) by using the entries of the n-tuple as the coefficients of a linear combination of \( {\bf u}_1 , {\bf u}_2 , \ldots , {\bf u}_n . \) This fact suggests that V is like the n-dimensional vector space \( \mathbb{R}^n , \) where n is the number of vectors in the basis for V.

Orthogonal Coordinate Systems

Although orthogonality is a opic of Part 5 of this tutorial, we discuss orthogonal systems over here because of its importance. Most likely you are familiar with dot product of two vectors, denoted by dot:
\[ {\bf x} \bullet {\bf y} = \left( x_1 , x_2 , \ldots , x_n \right) \bullet \left( y_1 , y_2 , \ldots , y_n \right) = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n \in \mathbb{R} , \]
where, for simplicity) we choose two vectors x, y from ℝn.

Linear Algebra for Computational Science and Engineering by F Nari page 158

 

 

  1. Find the coordinates of v with respect to the following bases:
    1. v = (2, −1), basis (2, 3), (3, −2) of ℝ².
    2. v = 1 − x², basis 1 + x, 2 −x, x −2x² of ℝ≤2[x].
    3. v = (2, −1), basis (1 + j, −1), (1, 1 −j) of ℂ².
    4. \( \displaystyle {\bf v} = \begin{bmatrix} 1&2 \\ 2&4 \end{bmatrix} , \) basis \( \displaystyle \begin{bmatrix} 0&2 \\ 2&3 \end{bmatrix} , \quad \begin{bmatrix} 2&0 \\ 0&1 \end{bmatrix} , \quad \begin{bmatrix} 0&0 \\ 0&1 \end{bmatrix} , \) of space of real symmetric 2×2 matrices.
  2. Find the coordinates of v with respect to the following bases:
    1. v = (1, 2, 3), basis (−1, 0, 1), (2, 1, 0), (3, 2, 1) od ℝ³.
    2. \( \displaystyle {\bf v} = \begin{bmatrix} 1&2 \\ -2&3 \end{bmatrix} , \) basis \( \displaystyle \begin{bmatrix} 3&4 \\ -4&3 \end{bmatrix} , \quad \begin{bmatrix} -1&1 \\ -1&2 \end{bmatrix} , \quad \begin{bmatrix} 3&3 \\-3&3 \end{bmatrix} , \) of the space of real skew symmetric 2×2 matrices.
    3. v = (1 + j, 1, 1-− j), basis (1, j, −1), (j, 1, −2), (0, 1, 2j) of ℂ³.
    4. v = (1 + c)², basis 1 −x², 2 + x, 3x + x². of ℝ≤2[x].
  3. Let V = span(v₁, v₂) , where v₁ = (1 − x)², v₂ = 2x + x². Find coordinates of u = 2 −10x −x² in V.
  4. Let Ei,j be a matrix with a one in the (i, j)th entry and zeros elsewhere. Which 2 × 2 matrices Ei,j can be added to the set below to form a basis of ℝ2×2: \[ {\bf A} = \begin{bmatrix} 0&1 \\ -1&0 \end{bmatrix} , \quad {\bf B} = \begin{bmatrix} 0&1 \\ 1&1 \end{bmatrix} , \quad {\bf C} = \begin{bmatrix} 1&1 \\ 0&0 \end{bmatrix} . \]
  5. Let Ei,j be a matrix with a one in the (i, j)th entry and zeros elsewhere. Which 2 × 2 matrices Ei,j can be added to the set below to form a basis of ℝ2×2: \[ {\bf A} = \begin{bmatrix} 1&1 \\ 1&0 \end{bmatrix} , \quad {\bf B} = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix} , \quad {\bf C} = \begin{bmatrix} 1&1 \\ 1&1 \end{bmatrix} . \]

  1. Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
  2. Fraleigh, J.B. and Beauregard, R.A., Linear Algebra, third edition, Addison Wesley Publication Company, New York, 1995.