To enhance pedagogical effectiveness, the treatment of the dot product is presented in several distinct sections
We denote by 𝔽 one of the following four fields: ℤ, a set of integers, ℚ, a set of rational numbers, ℝ, a set of real numbers, and ℂ, a set of complex numbers. However, in this section, we mostly use only one of them----the set of real numbers mostly because the definition of length or norm definition involves only ℝ (its extension for ℂ is discussed later in inner product section).
This section is devoted to one of the most important operations in all of linear algebra---dot product. Many operations and algorithms involve dot product, including convolution, correlation, matrix multiplication, duality, the Fourier transform, signal filtering, and many others.
Dot Product
We met many times in previous sections a special linear combination of numerical vectors. For instance, a linear equation in n unknownsRemark 1: Although textbooks on linear algebra define dot product for vectors of the same vector space (mostly because it leads to fruitfully theory and geometric applications), our definition extends the dot product for vectors from different vector spaces, but of the same dimension and over the same field 𝔽 of scalars. Importance of this definition stems from practical applications; for instance, in calculus you learn that the line integral involves definition of the dot product for vector field F with infinitesimal dr:
Let us make a numerical experiment by choosing the following matrices: \[ \mathbf{A}_1 = \begin{bmatrix} 1& 2.1 \\ -3& 2.2 \\ -3& -1.5 \end{bmatrix}, \quad \mathbf{A}_2 = \begin{bmatrix} -4& 1.3 \\ 1& 2.6 \\ 5& -3.1 \end{bmatrix}, \quad \mathbf{A}_3 = \begin{bmatrix} 2& 1.7 \\ 2& 6.2 \\ 8& 3.9 \end{bmatrix} . \] Then their dot product will be \[ \mathbf{a} \bullet \mathbf{b} = \begin{bmatrix} -3.& 10.6 \\ -5.& 18. \\ 9.& -6.8 \end{bmatrix} . \]
Remark 2: In applications, numerical vectors are usually associated with measurements and so inherit units. For instance, integer 5 is associated with 5 millions of dollars in Wall street offices, the same number is considered as a 5 dollars bill by a bank's clerk, but mechanical engineer may look at it as 5 centimeters, and computer science folks consider this information as 5 GB. Only mathematicians see in 5 an integer or number without any unit. Therefore, vectors and scalars in Linear Algebra are not related to any specific unit measurements. Now we all appreciate the beauty of mathematical language because we enter our particular information into a computer---this device recognizes only electric pulses as on or off---there is no room for any unit. When Joseph Fourier (1768--1830) introduced the Fourier transform in 1822
If s represents a displacement (e.g., it has SI units in meters) and f represents a force (e.g., with units in Newtons), then f • s represents a work (in Newton-meters or Joules). Therefore, the force has units of "Joules per meter".
The dot product of force (F) and velocity (v in meter per second) is called instantaneous power (or simply power). It represents the rate at which work is done by a force on an object and is a scalar quantity.
Electric flux density, denoted by D and measured in coulombs per square meter (C/m²), describes how electric displacement is distributed in space. In a linear, isotropic medium it is related to the electric field by \[ \mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}. \] This expression separates the response of the vacuum from the response of the material. The constant ε₀ ≈ 8.854187 × 10⁻¹² F m⁻¹, the permittivity of free space, has units C/(V·m) and determines how strongly the vacuum itself “permits’’ electric field lines. The vector P, the polarization, has units C/m² and represents the dipole moment per unit volume created when the molecules of a dielectric shift slightly under the influence of an electric field. Thus, ε₀E describes the field’s effect in empty space, while P encodes the additional displacement arising from bound charges inside matter.
Electric flux is defined through the dot product of the electric field with the unit normal n to a surface, \[ {\text d}\Phi_E = \mathbf{E}\bullet \hat{\bf n}\, {\text d}A. \] The dot product plays two essential roles. Geometrically, it selects only the component of E perpendicular to the surface, ensuring that tangential field components do not contribute to flux. Dimensionally, it preserves the units of E (V/m), and multiplication by area dA produces flux with units volt·meter (V·m). This construction shows how the combination of vector projection and area naturally yields a physically meaningful scalar quantity.
A parallel structure holds for D. Its surface integral, \[ \iint_S \mathbf{D}\bullet \hat{\bf n}\, {\text d}A = Q_{\mathrm{free}}, \] produces free charge (C). Again, the dot product ensures that only the normal component of D contributes, and the units combine cleanly: C/m² multiplied by m² yields C. This result is the content of Gauss’s law in matter, \[ \nabla \bullet \mathbf{D}=\rho_{\mathrm{free}}, \] which states that the divergence of D counts only free charge, because the bound charge associated with polarization has already been absorbed into P.
In vacuum or in a uniform linear dielectric, one may combine ε₀E and P into a single term ε E, so that D = ε E. In such cases D can be eliminated without loss of generality. However, in real materials—especially those with spatially varying permittivity or nonlinear polarization—D becomes indispensable. It provides a clean separation between the intrinsic electric field E and the material’s response P, with the dot product serving as the mathematical bridge that connects vector fields, geometry, and physical units.
The same geometric and dimensional structure appears in other areas of physics. Tor instance, magnetic flux (ΦB) measures the total magnetic field B passing through a surface and is defined by \[ {\text d}\Phi _B = \mathbf{B}\bullet \hat{\bf n}\, {\text d}A. \] Its SI unit is the weber (Wb), equal to tesla·meter² (T·m²), since B has units of tesla and dA has units of m². In fluid mechanics, the normal momentum flux is \[ \Pi =\rho \, (\mathbf{v}\bullet \mathbf{n}), \] with units kg/(m·s²), the same as pressure. In heat transfer, the rate of heat flow through a surface is \[ \dot {Q} = \mathbf{q}\bullet \hat{\bf n}\, {\text d}A, \] where q is the heat‑flux vector with units W/m², so that \( \displaystyle \quad \dot {Q} \quad \) has units of watts (W).
Across electromagnetism, fluid mechanics, and heat transfer, the dot product plays the same conceptual role: it extracts the normal component of a vector field and ensures that the resulting flux carries the correct physical dimensions. This unified structure explains why flux laws across physics share a common mathematical form, even though the underlying fields—electric, magnetic, momentum, or thermal—represent very different physical phenomena.
In continuum mechanics, the stress tensor acts on a surface with unit normal n = (n₁, n₂, n₃) to produce the traction vector t, which is the force per unit area acting on that surface. \[ \mathbf{t}=\left( \begin{matrix}\sigma _{11}n_1+\sigma _{12}n_2+\sigma _{13}n_3\\ \sigma _{21}n_1+\sigma _{22}n_2+\sigma _{23}n_3\\ \sigma _{31}n_1+\sigma _{32}n_2+\sigma _{33}n_3\end{matrix}\right) . \] This is a tensor–vector dot product, producing a vector. In index notation: \[ t_i =\sigma _{ij}n_j . \] Stress tensor units are N/m², while nornal vector is dimensionless. This tensor-vector product is one of the most important formulas in elasticity and continuum mechanics. ■
Remark 3: Recall that two vector spaces V and U are isomorphic (denoted V ≌ U) if there is a bijective linear map between them. This bijection (which is one-to-one and onto mapping) can be achieved by considering ordered bases α = [ a₁, a₂, … , an ] and β = [ b₁, b₂, … , bn ] in these vector spaces V and U, respectively. Then components of every vector with respect to a chosen ordered basis can be identified uniquely with an n-tuple. Therefore, the algebraic formula \eqref{EqDot.2} is essentially applied to two isomorphic copies of the Cartesian product 𝔽n. Geometric interpretation of the dot product, which is coordinate independent and therefore conveys invariant properties of these products, is given in the Euclidean space section.
Note: The definition of the dot product does not restrict applying it to two distinct isomorphic versions of the direct product 𝔽n ≅ 𝔽n×1 ≅ 𝔽1×n. It is the basic computational building-block from which many operations and algorithms are built. So you can find the dot product of a row vector with a column vector. However, we try to avoid writing it as matrix multiplication,
Mathematica is smart and does not distinguish rows from columns to some extend. Dot product can be accomplished with two Mathematica commands:
Dot[a, b]
a . b

One of the main and fruitful applications of the dot product is observed when scalar product involves numerical vectors from 𝔽n or their isomorphic copies. Upon introducing an ordered basis α = [e₁, e₂, … , en] in a finite dimensional vector space V, every its vector v = c₁e₁ + c₂e₂ + ⋯ + cnen is uniquely identified with the corresponding coordinate vector ⟦v⟧α = (c₁, c₂, … , cn) ∈ 𝔽n.
Calculate the dot product of two three dimensional vectors a = (3, 2, 1) and b = (4, −5, 2).
Solution: Using the component formula (1) for the dot product of three-dimensional vectors \[ \mathbf{a} \bullet \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 , \] we calculate the dot product to be \[ \mathbf{a} \bullet \mathbf{b} = 3 \cdot 4 - 2 \cdot 5 + 1 \cdot 2 = 4. \]
Dot[a, b]
Mathematica uses two commands for evaluation scalar products:
a.b
a.b
Not every curvilinear system of coordinates supports dot product, as the following example shows.
Definition of dot product in polar coordinates is presented in section "Dot product in coordinate systems" and Example 23. ■
Properties of dot product
The basic properties (1--4) of the dot product are valid for vectors from the same vector space, but the last one involves compatible vector dimensions. In presented properties, u, v, and w are finite dimensional vectors, and λ is a number (scalar):
- u • u > 0 and u • u = 0 if and only if u = 0.
- u • v = v • u (commutative law);
- (u + v) • w = u • w + v • w (distributive law);
- (λ u) • v = λ (u • v) = u • (λ v) (associative law);
-
for any two column vectors u ∈ ℝn×1, v ∈ ℝm×1, and matrix A ∈ ℝm×n, the following equation holds:
v • Au = ATv • u, where AT (A′) is the transpose of matrix A.
A similar relation holds for row vectors: u • vA = uAT • v.
- This property is trivial because \[ \mathbf{u} \bullet \mathbf{u} = u_1^2 + u_2^2 + \cdots + u_n^2 > 0 \] unless all components of vector u are zeroes.
- Applying the definition of dot product to u · v and v · u, we obtain \begin{align*} \mathbf{u} \bullet \mathbf{v} &= u_1 v_1 + u_2 v_2 + \cdots + u_n v_n \\ \mathbf{v} \bullet \mathbf{u} &= v_1 u_1 + v_2 u_2 + \cdots + v_n u_n \end{align*} Since product of two numbers from field 𝔽 is commutative, we conclude that u · v = v · u.
- Since every finite dimensional vector space is isomorphic to 𝔽n, we can assume that these vectors u, v, and w belong to the direct product 𝔽n. Then \[ \mathbf{u} + \mathbf{v} = \left( u_1 , \ldots , u_n \right) + \left( v_1 , \ldots , v_n \right) = \left( u_1 + v_1 , \ldots , u_n + v_n \right) . \] Taking the dot product with w, we get \begin{align*} \left( \mathbf{u} + \mathbf{v} \right) \bullet \mathbf{w} &= \left( u_1 + v_1 , u_2 + v_2 , \ldots , u_n + v_n \right)\left( w_1 , \ldots , w_n \right) \\ &= u_1 w_1 + v_1 w_1 + \cdots u_n w_n + v_n w_n \\ &= \mathbf{u} \bullet \mathbf{w} + \mathbf{v} \bullet \mathbf{w} . \end{align*}
- The left-hand side is \[ \left( \lambda\,\mathbf{u} \right) \bullet \mathbf{v} = \lambda\,u_1 v_1 + \cdots + \lambda u_n v_n = \lambda \left( u_1 v_1 + \cdots + u_n v_n \right) , \] which equal to the right-hand side λ (u • v).
- For matrix A = [𝑎i,j] ∈ ℝm×n, we have \[ \mathbf{v} \bullet \mathbf{A}\,\mathbf{u} = \sum_{i=1}^m v_i \left( \mathbf{A}\,\mathbf{u} \right)_i \] where the i-th component of A u is \[ \left( \mathbf{A}\,\mathbf{u} \right)_i = \sum_{j=1}^n a_{i.j} u_j . \] Changing the order of summation, we get \begin{align*} \mathbf{v} \bullet \mathbf{A}\,\mathbf{u} &= \sum_{i=1}^m v_i \sum_{j=1}^n a_{i.j} u_j \\ &= \sum_{j=1}^n \sum_{i=1}^m v_i a_{i.j} u_j = \sum_{j=1}^n u_j \left( \mathbf{A}^{\mathrm T} \mathbf{v} \right)_j , \end{align*} which is u • (ATv).
Note that the associative law for scalar product (v • u) • w ≠ v • (u • w) is not valid in general; see the following example.
-
Any nonzero vector will work; for instance, v = (3, −2, 1) ∈ ℝ³. Then
\[
\mathbf{v} \bullet \mathbf{v} = 3^2 + (-2)^2 + 1^2 = 9+4+1 = 14 > 0.
\]
{3, -2, 1} . {3, -2, 1}14
-
Commutativity holds because the dot product is implemented element-
wise, and each element-wise multiplication is simply the product
of two scalars. Scalar multiplication is commutative, and therefore the dot product is commutative.
Let \[ \mathbf{v} = \left( 1, 2, 3 \right) , \quad \mathbf{u} = \left( 4, -6, 5 \right) \in \mathbb{R}^3 . \] Then their scalar product is 7, independently of the order of multiplication,as Mathematica confirms:
v = {1, 2, 3}; u = {4, -6, 5}; v.u7Dot[u, v]7 -
Suppose we need to find a dot product of two numerical vectors v • u, one of which has large entries. For instance,
\[
\mathbf{v} = \begin{pmatrix} 3791 \\ -5688 \\ 2894 \end{pmatrix} , \quad \mathbf{u} = \begin{pmatrix} 3 \\ 2 \\ 4 \end{pmatrix} .
\]
Scalar product of these numerical vectors involves large unpleasant multiplications and summation. Using distributive property, we break vector v into sum of four vectors:
\[
\mathbf{v} = \mathbf{v}_1 + \mathbf{v}_2 + \mathbf{v}_3 + \mathbf{v}_4 ,
\]
where
\[
\mathbf{v}_1 = \begin{pmatrix} 1 \\ -8 \\ 4 \end{pmatrix} , \ \mathbf{v}_2 = \begin{pmatrix} 90 \\ -80 \\ 90 \end{pmatrix} , \ \mathbf{v}_3 = \begin{pmatrix} 700 \\ -600 \\ 800 \end{pmatrix} , \ \mathbf{v}_4 = \begin{pmatrix} 3000 \\ -5000 \\ 2000 \end{pmatrix} .
\]
The corresponding four scalar products are not tedious to find:
u = {3,2,4}; v1 = {1,-8,4}; v2 = {90, -80, 90}; v3 = {700,-600,800}; v4 = {3000,-5000,2000}; d1 = u.v13d2 = u.v2470d3 = u.v34100d4 = u.v47000Adding these four numbers, we get the required dot product: \begin{align*} \mathbf{v} \bullet \mathbf{u} &= \left( \mathbf{v}_1 + \mathbf{v}_2 + \mathbf{v}_3 + \mathbf{v}_4 \right) \bullet \mathbf{u} = \mathbf{v}_1 \bullet \mathbf{u} + \mathbf{v}_2 \bullet \mathbf{u} + \mathbf{v}_3 \bullet \mathbf{u} + \mathbf{v}_4 \bullet \mathbf{u} \\ &= 3+470+4100+7000 = 11573 . \end{align*}d1+d2+d3+d411573
-
We set λ = 3.1415926, v = (236, -718), u = (892, 435). Without computer assistance determination of corresponding dot products will be time consuming. So we ask Mathematica for help and find that
\[
\left( \lambda\mathbf{u} \right) \bullet \mathbf{v} = \lambda \left( \mathbf{u} \bullet \mathbf{v} \right) = \mathbf{u} \bullet \left( \lambda \mathbf{v} \right) \approx 319871.
\]
la =3.1415926; v = {236,-718}; u = {892, 435}; (la*u) . v319871.u . (la*v)319871.la*(v . u)319871.
-
Let us take a singular matrix and two 3-column vectors:
\[
\mathbf{A} = \begin{bmatrix} 1&2&3 \\ 4&5&6 \\ 7&8&9 \end{bmatrix} , \quad \mathbf{u} = \begin{pmatrix} 35 \\ -11 \\ 17 \end{pmatrix} , \quad \mathbf{v} = \begin{pmatrix} 23 \\ 97 \\ 41 \end{pmatrix} .
\]
A = {{1, 2, 3}, {4, 5, 6}, {7,8 ,9}};We set vectors v and u as 3-tuples (elements of ℝ³) but not column vectors (elements of ℝ3×1) because Mathematica is smart to understand that we want column vectors.
u = {35,-11,17}; v = {23,97,41};u = {{35}, {-11}, {17}}; v = {{23}, {97}, {41}};
Dot[u, A . v]25049andDot[Transpose[A] . u, v]25049Now we check the same property for row vectors:Dot[u . A, v]25049Dot[v . Transpose[A], u]25049Rectangular matrix: we consider 3-by-2 matrix \[ \mathbf{A} = \begin{bmatrix} 1&2 \\ 3&4 \\ 5&6 \end{bmatrix} \] and two column vectors \[ \mathbf{u} = \begin{pmatrix} a \\ b \end{pmatrix}, \qquad \mathbf{v} = \begin{pmatrix} c \\ d \\ e \end{pmatrix} . \] Then \[ \mathbf{A}\,\mathbf{u} = \begin{bmatrix} 1&2 \\ 3&4 \\ 5&6 \end{bmatrix}\begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} 1\cdot a + 2 \cdot b \\ 3 \cdot a + 4 \cdot b \\ 5 \cdot a + 6 \cdot b \end{pmatrix} . \] Its dot product with v becomes \[ \mathbf{v} \bullet \mathbf{A}\,\mathbf{u} = c \left( a + 2\,b \right) + d \left( 3\,a + 4\, b \right) + e \left( 5\,a + 6\, b \right) . \tag{A} \] On the other hand, \[ \mathbf{A}^{\mathrm T} \mathbf{v} = \begin{bmatrix} 1 & 3 & 5 \\ 2&4&6 \end{bmatrix} \begin{pmatrix} c \\ d \\ e \end{pmatrix} = \begin{pmatrix} 1\cdot c + 3\cdot d + 5\cdot e \\ 2 \cdot c + 4 \cdot d + 6 \cdot e \end{pmatrix} . \] Then its dot product with u becomes \[ \mathbf{A}^{\mathrm T} \mathbf{v} \bullet \mathbf{u} = a \left( c + 3\, d + 5\, e \right) + b \left( 2\,c + 4\, d + 6\, e \right) . \tag{B} \] Do you need a computer assistance to check that expression (A) is the same as (B) ? I don't need it.
-
Extra warning:
We demonstrate that the identity v • (u • w) = (v • u) • w is not valid for arbitrary vectors v, u, and w. It is true only when v is a scalar multiple of w. Indeed, let k = u • w and c = v • u. Then
\[
\mathbf{v} \bullet \left( \mathbf{u} \bullet \mathbf{w} \right) = \left( \mathbf{v} \bullet \mathbf{u} \right) \bullet \mathbf{w} \quad \iff \quad \mathbf{v} k = c \mathbf{w} .
\]
from the latter, it follows that vectors v and w are collinear.
We choose three vectors (and write them in column form): \[ \mathbf{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \quad \mathbf{u} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} , \quad \mathbf{w} = \begin{pmatrix} 5 \\ 6 \end{pmatrix} . \] Then \[ \mathbf{v} \bullet \left( \mathbf{u} \bullet \mathbf{w} \right) = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \cdot 39 = \begin{pmatrix} 39 \\ 78 \end{pmatrix} \]
v = {1, 2}; u = {3, 4}; w = {5, 6};
u . w39v*39{39, 78}and \[ \left( \mathbf{v} \bullet \mathbf{u} \right) \bullet \mathbf{w} = 11 \cdot \begin{pmatrix} 5 \\ 6 \end{pmatrix} = \begin{pmatrix} 55 \\ 66 \end{pmatrix} . \]Dot[v, u]1111*w{55, 66}However, for some vectors, we observe v • (u • w)) = (v • u) • w. Let us pick up three vectors \[ \mathbf{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \quad \mathbf{u} = \begin{pmatrix} 3 \\ 5 \end{pmatrix} , \quad \mathbf{w} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} . \] Then \[ \mathbf{v} \bullet \left( \mathbf{u} \bullet \mathbf{w} \right) = \mathbf{v} \,26 = 26 \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \]v = {1, 2}; u = {3,5}; w = {2,4}; u.w26and \[ \left( \mathbf{v} \bullet \mathbf{u} \right) \bullet \mathbf{w} = 13 \mathbf{w} = 13 \begin{pmatrix} 2 \\ 4 \end{pmatrix} . \]v.u13Since \[ 26 \begin{pmatrix} 1 \\ 2 \end{pmatrix} = 13 \begin{pmatrix} 2 \\ 4 \end{pmatrix} , \] we conclude that this identity is valid for collinear vectors v, and w, and arbitrary u.
It is convenient to introduce the following notation: ∥v∥² = v • v. Positive square root of this quantity is call the norm in mathematics. Then Cauchy inequality can be rewritten as \[ \left\vert {\bf u} \bullet {\bf v} \right\vert \le \| {\bf u} \| \cdot \| {\bf v} \| , \] Suppose first that either u or v is zero. Then their dot product is zero and the Cauchy inequality holds.
Now suppose that neither u nor v is zero. It follows that ∥u∥ > 0 and ∥v∥ > 0 because the dot product x • x > 0 for any nonzero vector x. We have \begin{align*} 0 &\le \left( \frac{{\bf u}}{\| {\bf u} \|} + \frac{{\bf v}}{\| {\bf v} \|} \right) \bullet \left( \frac{{\bf u}}{\| {\bf u} \|} + \frac{{\bf v}}{\| {\bf v} \|} \right) \\ &= \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf u}}{\| {\bf u} \|} \right) + 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + \left( \frac{{\bf v}}{\| {\bf v} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) \\ &= \frac{1}{\| {\bf u} \|^2} \left( {\bf u} \bullet {\bf u} \right) + \frac{2}{\| {\bf u} \| \cdot \| {\bf v} \|} \left( {\bf u} \bullet {\bf v} \right) + \frac{1}{\| {\bf v} \|^2} \left( {\bf v} \bullet {\bf v} \right) \\ &= \frac{1}{\| {\bf u} \|^2} \, \| {\bf u} \|^2 + 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + \frac{1}{\| {\bf v} \|^2} \, \| {\bf v} \|^2 \\ &= 1 + 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + 1 \end{align*} Hence, −∥u∥ · ∥v∥ ≤ u • v. Similarly, \begin{align*} 0 &\le \left( \frac{{\bf u}}{\| {\bf u} \|} - \frac{{\bf v}}{\| {\bf v} \|} \right) \bullet \left( \frac{{\bf u}}{\| {\bf u} \|} - \frac{{\bf v}}{\| {\bf v} \|} \right) \\ &= \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf u}}{\| {\bf u} \|} \right) - 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + \left( \frac{{\bf v}}{\| {\bf v} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) \\ &= \frac{1}{\| {\bf u} \|^2} \left( {\bf u} \bullet {\bf u} \right) - \frac{2}{\| {\bf u} \| \cdot \| {\bf v} \|} \left( {\bf u} \bullet {\bf v} \right) + \frac{1}{\| {\bf v} \|^2} \left( {\bf v} \bullet {\bf v} \right) \\ &= \frac{1}{\| {\bf u} \|^2} \, \| {\bf u} \|^2 - 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + \frac{1}{\| {\bf v} \|^2} \, \| {\bf v} \|^2 \\ &= 1 - 2 \left( \frac{{\bf u}}{\| {\bf u} \|} \bullet \frac{{\bf v}}{\| {\bf v} \|} \right) + 1 \end{align*} Therefore, u • v ≤ ∥u∥ · ∥v∥. By combining the two inequalities, we obtain the Cauchy inequality.
The case n = 1 is trivially true. When n = 2, Cauchy’s inequality just says \[ \left( a_1 b_1 + a_2 b_2 \right)^2 \leqslant \left( a_1^2 + a_2^2 \right) \left( b_1^2 + b_2^2 \right) . \] Expanding both sides to find the equivalent inequality \[ 0 \leqslant \left( a_1 b_2 \right)^2 - 2 \left( a_1 b_2 a_2 b_1 \right) + \left(a_2 b_1 \right)^2 . \] From the well-known factorization x² − 2xy + y² = (x − y)² one finds \[ 0 \leqslant \left( a_1 b_2 - a_2 b_1 \right)^2 , \] and the nonnegativity of this term confirms the truth of Cauchy's inequality for n = 2.
Now that we have proved a nontrivial case of Cauchy’s inequality, we are ready to look at the induction step. If we let H(n) stand for the hypothesis that Cauchy’s inequality is valid for n, we need to show that H(2) and H(n) imply H(n + 1). With this plan in mind, we do not need long to think of first applying the hypothesis H(n) and then using H(2) to stitch together the two remaining pieces. Specifically, we have \begin{align*} & \quad a_1 b_1 + a_2 b_2 + \cdots + a_n b_n + a_{n+1} b_{n+1} \\ &= \left( a_1 b_1 + a_2 b_2 + \cdots + a_n b_n \right) + a_{n+1} b_{n+1} \\ & \leqslant \left( a_1^2 + a_2^2 + \cdots + a_n^2 \right)^{1/2} \left( b_1^2 + b_2^2 + \cdots + b_n^2 \right)^{1/2} + a_{n+1} b_{n+1} , \\ & \leqslant \left( a_1^2 + a_2^2 + \cdots + a_n^2 + a_{n+1}^2 \right)^{1/2} \left( b_1^2 + b_2^2 + \cdots + b_n^2 + b_{n+1}^2 \right)^{1/2} \end{align*} where in the first inequality, we used the inductive hypothesis H(n) and in the second inequality we used H(2) in the form \[ \alpha \beta + a_{n+1} b_{n+1} \leqslant \left( \alpha^2 + a_{n+1}^2 \right)^{1/2} \left( \beta^2 + b_{n+1}^2 \right)^{1/2} , \] with the new variables \[ \alpha = \left( a_1^2 + a_2^2 + \cdots + a_n^2 \right)^{1/2} , \quad \beta = \left( b_1^2 + b_2^2 + \cdots + b_n^2 \right) . \]
Now we set vector u to be u = 2.71828 v. Using Mathematica, we repeat all previous calculations for these two vectors.
Equality: We consider two vectors in ℝ²: \[ \mathbf{v} = \left( 1 , 2 \right) , \qquad \mathbf{u} = \left( 2 , 4 \right) \] They are linearly dependent because u = 2v. Their scalar product is \[ \left( 1 , 2 \right) \bullet \left( 2 , 4 \right) = 1 \cdot 2 + 2 \cdot 4 = 10. \] I hope that you can square this number without a computer assistance. Norms squared of these vectors are \[ \| \mathbf{v} \|^2 = 1^2 + 2^2 = 5 , \qquad \| \mathbf{u} \|^2 = 2^2 + 4^2 = 4 + 16 = 20 . \] Their product becomes \[ \| \mathbf{v} \|^2 \cdot \| \mathbf{u} \|^2 = 5 \cdot 20 = 100 = 10^2 = \left( \mathbf{v} \bullet \mathbf{u} \right)^2 . \] ■
Important Note: Cauchy's inequality is not valid for complex vector spaces as the following example shows for two 2-vectors u = (1, j) and v = (1, −j), where j is the imaginary unit vector of the complex plane ℂ so j² = −1.
The inequality \eqref{EqDot.3} is also referred to as the Cauchy--Schwarz or Cauchy--Bunyakovsky--Schwarz or usually as CBS inequality.
The inequality \eqref{EqDot.3} was first proved by the French mathematician, engineer, and physicist baron Augustin-Louis Cauchy in 1821. In 1859, Victor Bunyakovsky extended this inequality to the case of infinite summation, that is, he established the integral version of the Cauchy inequality. Contribution of Hermann Schwarz (1843--1921) to the Cauchy inequality is unknown neither to me nor to AI except that he married a daughter of the famous mathematician Ernst Eduard Kummer. In 1888, about 30 years after Bunyakovsky's publication, Hermann presented a proof similar to Bunyakovsky's one,
 |
 |
 |
||
|---|---|---|---|---|
| Augustin-Louis Cauchy | Victor Yakovlevich Bunyakovsky | Hermann Amandus Schwarz |
The first step toward the Bunyakovsky result is to establish inequality
For any n ∈ ℕ, define the partial sums \[ S_n = \sum _{k=1}^n a_k b_k. \] By the usual (finite) Cauchy–Schwarz inequality, \[ \left( \sum _{k=1}^na_k b_k\right) ^2 \leq \left( \sum _{k=1}^n a_k^2\right) \left( \sum_{k=1}^n b_k^2\right) . \] So \[ S_n^2 \leq A_n B_n,\quad A_n:=\sum _{k=1}^n a_k^2,\quad B_n :=\sum _{k=1}^n b_k^2. \]
Step 2: Use convergence of \( \displaystyle \quad \sum a_k^2 \quad \& \quad \sum b_k^2 . \)
Assume \[ \sum _{k=1}^{\infty }a_k^2 <\infty ,\qquad \sum _{k=1}^{\infty }b_k^2 <\infty . \] Then (Aₙ) and (Bₙ) are increasing and bounded, hence converge: \[ A_n\rightarrow A:=\sum _{k=1}^{\infty }a_k^2,\qquad B_n\rightarrow B:=\sum _{k=1}^{\infty }b_k^2. \] From the finite inequality, \[ |S_n|\leq \sqrt{A_nB_n}\leq \sqrt{AB}\quad \mathrm{for\ all\ }n. \] So (Sₙ) is a bounded sequence.
Step 3: Show \( \displaystyle \quad \sum a_kb_k \quad \) converges (Cauchy criterion).
For .m > n, \[ S_m-S_n=\sum _{k=n+1}^ma_kb_k. \] Apply finite Cauchy–Schwarz to the finite sum from k=n+1 to m: \[ \left| \sum _{k=n+1}^m a_kb_k\right| \leq \left( \sum _{k=n+1}^ma_k^2\right) ^{1/2}\left( \sum _{k=n+1}^mb_k^2\right) ^{1/2}. \] Let \[ A_{n,m}:=\sum _{k=n+1}^ma_k^2,\quad B_{n,m}:=\sum _{k=n+1}^mb_k^2. \] Then \[ |S_m-S_n|\leq \sqrt{A_{n,m}B_{n,m}}. \] Since \( \displaystyle \quad \sum a_k^2 \quad\& \quad \sum b_k^2 \quad \) converge, their tails go to zero: \[ \sum _{k=n+1}^{\infty }a_k^2\rightarrow 0,\quad \sum _{k=n+1}^{\infty }b_k^2\rightarrow 0\quad \mathrm{as\ }n\rightarrow \infty . \] Thus, for any ε > 0, choose N such that for all n ge; N, \[ \sum _{k=n+1}^{\infty }a_k^2<\varepsilon ^2,\quad \sum _{k=n+1}^{\infty }b_k^2<\varepsilon ^2. \] Then for all m > n ≥ N, \[ A_{n,m}\leq \sum _{k=n+1}^{\infty }a_k^2<\varepsilon ^2,\quad B_{n,m}\leq \sum _{k=n+1}^{\infty }b_k^2<\varepsilon ^2, \] so \[ |S_m-S_n|\leq \sqrt{A_{n,m}B_{n,m}}<\sqrt{\varepsilon ^2\varepsilon ^2}=\varepsilon ^2. \] Hence, (Sₙ) is a Cauchy sequence, so it converges. Therefore, \[ \sum _{k=1}^{\infty }a_kb_k \] converges, and we may define \[ S := \sum_{k\ge 1} a_k b_k = \lim_{n\to\infty} S_n . \]
Step 4: Pass to the limit in the inequality.
From the finite inequality \[ S_n^2\leq A_nB_n, \] take limits as n → ∞: \[ \left( \sum _{k=1}^{\infty }a_kb_k\right) ^2=\lim _{n\rightarrow \infty }S_n^2\leq \lim _{n\rightarrow \infty }A_nB_n=\left( \sum _{k=1}^{\infty }a_k^2\right) \left( \sum _{k=1}^{\infty }b_k^2\right) . \] So we obtain the desired extension under the assumptions \[ \sum _{k=1}^{\infty }a_k^2<\infty ,\quad \sum _{k=1}^{\infty }b_k^2<\infty . \]
A positive definite matrix with real entries is a symmetric matrix where all of its eigenvalues are strictly positive. This means that when the matrix is applied to any non-zero vector, it results in a vector that is scaled and not reflected or reduced to zero. In simpler terms, it represents a transformation that only stretches vectors and doesn't flip them or collapse them to a single point.
Another matrix: We repeat all previous calculations with another not positive definite matrix \[ \mathbf{A} = \begin{bmatrix} -249& -292& -276& 412 \\ 136& 161& 150& -226 \\ 185& 218& 205& -308 \\ 69& 82& 76& -115 \end{bmatrix} . \] Its characteristic polynomial is det(λI − A) = (λ − 1)³(λ + 1). The corresponding dot products are
The following assessment provides a matrix version of Cauchy's inequality. Recall that |·| = det(·) denotes the determinant of a square matrix.
- rank(A) < n or rank(B) < n;
- B = A C for some nonsingular matrix C.
For the remainder of the proof assume \[ \left\vert\mathbf{A}^{\mathrm T}\mathbf{B}\right\vert \neq 0. \] In particular, both A and B must have full column rank n.
Step 1: Singular value decompositions yields \[ \mathbf{A} = \mathbf{P}_1 \mathbf{D}_1 \mathbf{Q}_1 , \qquad \mathbf{B} = \mathbf{P}_2 \mathbf{D}_2 \mathbf{Q}_2 , \] where
- P₁, P₂ are m × n matrices with orthonormal columns, i.e., PT₁P₁ = Iₙ and PT₂P₂ = Iₙ, the identity n×n matrix;
- Q₁, Q₂ are n-by-n orthogonal matrices;
- D₁, D₂ are diagonal n-by-n matrices with positive diagonal entries (the singular values).
Step 2: Why |PT₁P₂| ≤ 1.
The matrices P₁ and P₂ have orthonormal columns, so they each represent an orthonormal basis of an n-dimensional subspace of ℝm, W₁ ⊆ ℝm and W₂ ⊆ ℝm, respectively. The matrix \[ \mathbf{M} = \mathbf{P}_1^{\mathrm T} \mathbf{P}_2 \] is the change‑of‑basis matrix between these two orthonormal bases.
A fundamental fact from the theory of principal angles between subspaces states:
The singular values of M are cosθ₁ , … , cosθₙ, where θ₁, … , θₙ are the principal angles between the column spaces of P₁ and P₂.
Thus \[ |\mathbf{M}|=\prod _{k=1}^n\cos \theta _k. \] Since |cosθk| ≤ 1 for each k, \[ \left\vert \mathbf{P}_1^{\mathrm T}\mathbf{P}_2 \right\vert \leq 1. \]
We can also give an algebraic explanation of inequality |PT₁P₂| ≤ 1, which is based on Hadamard’s inequality: \[ |\mathbf{M}|\leq \prod _{j=1}^n \left\| \mathbf{M}_j \right\| , \qquad \forall \mathbf{M} \in \mathbb{R}^{n\times n} , \] where Mj are the column vectors. Apply this to M = PT₁P₂:
- Each column of M is PT₁pj, where pj is a column of P₂.
- Since P₁ has orthonormal columns, PT₁ is a contraction: \[ \| \mathbf{P}_1^{\mathrm T}\mathbf{x}\| \leq \| \mathbf{x}\| . \]
- Each pj has norm 1 (because columns of P₂ are orthonormal).
Step 3: Equality conditions |PT₁P₂| = 1 occurs if and only if \[ \cos \theta_1 = \cdots = \cos \theta_n = 1, \] i.e., all principal angles are zero. This means the two subspaces coincide and the two orthonormal bases differ only by an orthogonal transformation: \[ \mathbf{P}_2 = \mathbf{P}_1 \mathbf{C},\qquad \mathbf{C}\in O(n). \] Returning to the SVD expressions, this implies \[ \mathbf{B} = \mathbf{A}\left( \mathbf{Q}_1^{\mathrm T}\mathbf{C}{\bf Q}_2 \right) , \] and the matrix in parentheses is nonsingular. Thus, \[ \mathbf{B} = \mathbf{A\,C} \] for some nonsingular matrix C.
Combining this with the earlier rank‑deficient case completes the proof.
Conclusion: The inequality \[ \left\vert \mathbf{A}^{\mathrm T}\mathbf{B}\right\vert^2 \leq \left\vert \mathbf{A}^{\mathrm T}\mathbf{A}\right\vert \, \left\vert \mathbf{B}^{\mathrm T}\mathbf{B} \right\vert \] is a determinantal analogue of the Cauchy–Schwarz inequality, and equality holds precisely when the column spaces of A and B coincide (up to an invertible transformation or when one of the matrices fails to have full column rank.

Its proof is based on Young’s inequality
This is a standard form of Young’s inequality. We provide three proofs of this inequality.
A. Proof of Young’s inequality based on convexity of t ↦ et.
Define \[ \phi (t)=e^t. \] This function is convex on ℝ, so for any λ ∈ [0, 1] and any x, y ∈ ℝ, \[ \phi (\lambda x+(1-\lambda )y)\; \leq \; \lambda \phi (x)+(1-\lambda )\phi (y). \] Take \[ \lambda =\frac{1}{p},\quad 1-\lambda =\frac{1}{q}, \] and choose \[ x=p\ln a,\quad y=q\ln b \] (with the convention that if 𝑎 = 0 or b = 0, the inequality is trivial). Then \[ \lambda x+(1-\lambda )y=\frac{1}{p}(p\ln a)+\frac{1}{q}(q\ln b)=\ln a+\ln b=\ln (ab). \] Applying convexity: \[ e^{\ln (ab)}=ab\; \leq \; \frac{1}{p}e^{p\ln a}+\frac{1}{q}e^{q\ln b}=\frac{1}{p}a^p+\frac{1}{q}b^q. \] This is exactly Young’s inequality.
Equality condition: Convexity of et is strict, so equality holds if and only if x = y, that is, \[ p\ln a=q\ln b\quad \Longleftrightarrow \quad \ln (a^p)=\ln (b^q)\quad \Longleftrightarrow \quad a^p=b^q. \]
B: Proof of Young’s inequality based on direct calculus.
Fix b ≥ 0 and define for 𝑎 ≥ 0: \[ f(a)=\frac{a^p}{p}+\frac{b^q}{q}-ab. \] We want to show f(𝑎) ≥ 0 for all 𝑎 ≥ 0. Compute the derivative: \[ f'(a)=a^{p-1}-b. \] Critical point: \[ f'(a)=0\quad \Longleftrightarrow \quad a^{p-1}=b\quad \Longleftrightarrow \quad a=b^{1/(p-1)}. \] Second derivative: \[ f''(a)=(p-1)a^{p-2}\geq 0, \] so f is convex and the critical point is a global minimum. Evaluate f at this point: \[ a=b^{1/(p-1)}. \] Note that q = p/(p-1). Then \[ f(a)=\frac{a^p}{p}+\frac{b^q}{q}-ab=\frac{b^q}{p}+\frac{b^q}{q}-b^{1/(p-1)}b=b^q\left( \frac{1}{p}+\frac{1}{q}-1\right) =b^q(1-1)=0. \] Since this is the global minimum and f(𝑎) ≥ 0 for all 𝑎, we obtain \[ ab\leq \frac{a^p}{p}+\frac{b^q}{q}, \] with equality if and only if 𝑎p-1 = b, i.e., 𝑎p = bq.
C: Proof of Young’s inequality based on Legendre transformation because the Legendre transform gives this inequality almost immediately.
Consider the convex function \[ \phi (x)=\frac{x^p}{p},\qquad x\geq 0. \] Its Legendre transform φ✶ is \[ \phi ^*(y)=\sup _{x\geq 0}\left( xy-\frac{x^p}{p}\right) . \] To find the maximizing x, differentiate: \[ \frac{\text d}{{\text d}x}\left( xy-\frac{x^p}{p}\right) =y-x^{p-1}. \] Set to zero: \[ y=x^{p-1}\quad \Longrightarrow \quad x=y^{1/(p-1)}. \] Plug this back into the expression: \[ \phi ^*(y)=xy-\frac{x^p}{p}=y^{\frac{1}{p-1}}y-\frac{1}{p}\left( y^{\frac{1}{p-1}}\right) ^p. \] Compute the exponents carefully. Since \[ \frac{1}{p-1}=\frac{q}{p}\quad \mathrm{because}\quad q=\frac{p}{p-1}, \] we have \[ y^{\frac{1}{p-1}}=y^{\frac{q}{p}}, \] and \[ \left( y^{\frac{1}{p-1}}\right) ^p=y^{\frac{p}{p-1}}=y^q. \] So \[ \phi ^*(y)=y^{\frac{q}{p}}y-\frac{1}{p}y^q=y^{\frac{q}{p}+1}-\frac{1}{p}y^q. \] But \[ \frac{q}{p}+1=\frac{q+p}{p}=\frac{\frac{p}{p-1}+p}{p}=\frac{\frac{p+p(p-1)}{p-1}}{p}=\frac{\frac{p+p^2-p}{p-1}}{p}=\frac{\frac{p^2}{p-1}}{p}=\frac{p}{p-1}=q, \] so \[ y^{\frac{q}{p}+1}=y^q. \] Therefore, \[ \phi ^*(y)=y^q-\frac{1}{p}y^q=\left( 1-\frac{1}{p}\right) y^q=\frac{1}{q}y^q. \] Hence, we have explicitly: \[ \phi (x)=\frac{x^p}{p},\qquad \phi ^*(y)=\frac{y^q}{q}. \] Now we apply the Fenchel–Young inequality \[ xy\; \leq \; \phi (x) +\phi ^*(y), \] which is valid for any convex function φ and its Legendre transform φ✶ and for all x, y ≥ 0, with equality if and only if \[ b=a^{p-1}\quad \Longleftrightarrow \quad a^p=b^q. \] Applying this inequality with our φ and φ✶ gives \[ xy\; \leq \; \frac{x^p}{p}+\frac{y^q}{q}. \] ▣
We will apply Young’s inequality componentwise.
Step 2: Normalization and application to each component.
Assume first that both u and v are nonzero. Define \[ A=\left( \sum _{i=1}^n|u_i|^p\right) ^{1/p},\qquad B=\left( \sum _{i=1}^n|v_i|^q\right) ^{1/q}. \] If either A = 0 or B = 0, then one of the vectors is the zero vector and the inequality is trivial, with equality.
Now define normalized sequences \[ x_i=\frac{|u_i|}{A},\qquad y_i=\frac{|v_i|}{B}. \] Then \[ \sum _{i=1}^nx_i^p=1,\qquad \sum _{i=1}^ny_i^q=1. \] Apply Young’s inequality to each pair (xi, yi): \[ x_i y_i \leq \frac{x_i^p}{p}+\frac{y_i^q}{q}. \] Summing over i from 1 to n, we obtain \[ \sum _{i=1}^nx_iy_i\; \leq \; \frac{1}{p}\sum _{i=1}^nx_i^p+\frac{1}{q}\sum _{i=1}^ny_i^q=\frac{1}{p}\cdot 1+\frac{1}{q}\cdot 1=1. \] Thus, \[ \sum _{i=1}^n\frac{|u_i|}{A}\cdot \frac{|v_i|}{B}\; \leq \; 1, \] or equivalently, \[ \sum _{i=1}^n|u_iv_i|\; \leq \; AB=\left( \sum _{i=1}^n|u_i|^p\right) ^{1/p}\left( \sum _{i=1}^n|v_i|^q\right) ^{1/q}. \] This is precisely Hölder’s inequality.
Step 3: Equality conditions.
We now analyze when equality holds. From the derivation, equality in Hölder’s inequality requires equality in Young’s inequality for each index i with xiyi ≠ 0. For a fixed i, equality in \[ x_iy_i\leq \frac{x_i^p}{p}+\frac{y_i^q}{q} \] holds if and only if \[ x_i^p=y_i^q. \] Thus, for all i such that ui ≠ 0 and vi ≠ 0, we must have \[ \left( \frac{|u_i|}{A}\right) ^p=\left( \frac{|v_i|}{B}\right) ^q. \] Equivalently, \[ \frac{|u_i|^p}{A^p}=\frac{|v_i|^q}{B^q}. \] Since \( \displaystyle \quad\sum _i|u_i|^p = A^p \quad\mbox{and}\quad \sum _i|v_i|^q = B^q, \quad \) this condition implies that the ratios |ui|p and |vi|q are proportional across all indices where both are nonzero. In particular, there exists a constant λ > 0 such that \[ |u_i|^p=\lambda \, |v_i|^q\quad \mathrm{for\ all\ }i\mathrm{\ with\ }u_iv_i\neq 0. \] Taking p-th and q-th roots, this means \[ |u_i|=c\, |v_i|\quad \mathrm{for\ some\ }c>0\mathrm{\ and\ all\ relevant\ }i. \] Including signs, this says that u and v are proportional componentwise, i.e., there exists a scalar α ∈ ℝ such that \[ u_i=\alpha \, v_i\quad \mathrm{for\ all\ }i, \] with the understanding that if some components vanish, the relation still holds globally.
Thus equality in Hölder’s inequality holds if and only if one vector is a scalar multiple of the other (or one of them is the zero vector, which is a degenerate case of the same statement).
Summary:
- Hölder’s inequality in \mathbb{R^{\mathnormal{n}}} follows from applying Young’s inequality componentwise to normalized sequences.
- The inequality \[ \sum _{i=1}^n|u_iv_i|\; \leq \; \left( \sum _{i=1}^n|u_i|^p\right) ^{1/p}\left( \sum _{i=1}^n|v_i|^q\right) ^{1/q} \] is thus a direct consequence of convexity.
- Equality holds precisely when u and v are linearly dependent, i.e. one is a scalar multiple of the other.
Using decomposition Theorem:
Let A and B be m × m symmetric matrices with B being positive definite. Let Λ = diag(λ₁, λ₂, … , λm), where λ₁, λ₂, … , λm are the eigenvalues of B−1A. Then a nonsingular matrix C exists, such that \[ \mathbf{C}\,\mathbf{A}\,\mathbf{C}^{\mathrm T} = \Lambda , \quad \mathbf{C}\,\mathbf{B}\,\mathbf{C}^{\mathrm T} = \mathbf{I}_m . \]
we can write A = T Λ Tt and B = T Tt, where T is a nonsingular matrix, Λ = diag(λ₁, λ₂, … , λn), and λ₁, λ₂, … , λn are the eigenvalues of B−1A, and Tt is transpose matrix. Thus, the proof will be complete if we can show that \[ \left\vert \Lambda \right\vert^{\alpha} = \prod_{i=1}^n \lambda_i^{\alpha} \leqslant \left\vert \alpha \Lambda + \left( 1 - \alpha \right) \mathbf{I}_n \right\vert = \prod_{i=1}^n \left( \alpha \lambda_i + 1 - \alpha \right) , \] with equality if and only if Λ = In. This result is easily confirmed by showing the function g(λ) = αλ + 1 − α − λα is minimized at λ = 1 when 0 ≤ α ≤ 1.
Dot Product and Linear Transformations
The fundamental significance of the dot product is that it is a linear transformation of vectors in each multiplier. This means that the function f(v) = u • v is a linear functional for any fixed vector u. Then scalar product can be defined as a bilinear form:
Applications
Scalar products are intimately associated with a variety of physical concepts. For example, if the vector is mean-centered---the average of all vector elements is subtracted from each element---then the dot product this vector with itself is called variance in statistics. So it provides a measurement of dispersion across a data set.Vector fields assign a vector (magnitude and direction) to every point in a space, commonly representing physical quantities like wind velocity, fluid flow, or electromagnetic forces. For simplicity, let us consider a 2D vector field F(x, y) = = ⟨ P(x, y), Q(x, y) ⟩ (you can think of it as the velocity of fluid flowing over the plane) and let C be a smooth oriented curve in the plane. At each point of the directed path C we introduce a unit tangent vector t in the direction of the curve C, and a unit normal vector n pointing to our right as we travel along C. Vector field F can be decomposed into tangential and normal components:
The work done by a force applied at a point serves as a primary example of dot product because the work is defined as the product of the displacement and the component of the force in the direction of displacement (i.e., the projection of the force onto the direction of the displacement). Thus, the component of the force perpendicular to the displacement "does no work." If F is the force (in Newtons) and s is the displacement (in meters), then the work W is by definition equal to
Naturally, other physical quantities can be expressed in such a way. For example, the electrostatic potential energy gained by moving a charge q along a path C in an electric field E is −q∫C E • dr. We may also note that Ampere's law concerning the magnetic field B associated with a current-carrying wire can be written as \[ \oint_C {\bf B} \bullet {\text d}{\bf r} = \mu_0 I , \] where I is the current enclosed by a closed path C traversed in a right-handed sense with respect to the current direction. ■
2D case: we start with flat (ℝ²).
The area of a 2D triangle whose vertices are 𝑎 = (x𝑎, y𝑎), b = (xb, yb), c = (xc, yc) (as shown in figure 1) is given by \[ \mbox{area} = \frac{1}{2} \begin{vmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{vmatrix} . \]
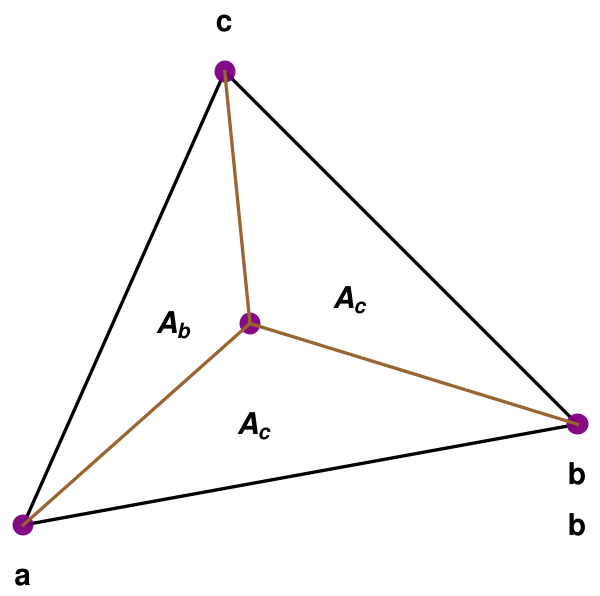
Barycentric coordinates allow us to express the coordinates of p = (x, y) in terms of 𝑎, b, c. More specifically, the barycentric coordinates of p are the numbers β and γ such that \[ p = a + \beta\left( b-a \right) + \gamma \left( c -a \right) \] If we regroup 𝑎, b, c, we obtain \begin{align*} p &= a + \beta\,b - \beta\,a + \gamma\,c - \gamma\,a \\ &= \left( 1 - \beta - \gamma \right) a + \beta\,b + \gamma\,c . \end{align*} It is customary to define a third variable α by \[ \alpha = 1 - \beta - \gamma . \] Then we have \[ p = \alpha\,a + \beta\, b + \gamma\,c , \qquad \alpha + \beta + \gamma = 1 . \] The barycentric coordinates of the point p in terms of the points 𝑎, b, c are the numbers α, β, γ such that p = α𝑎 + βb + γc, with α + β + γ = 1.
Barycentric coordinate are defined for all points in the plane. They have several nice features:
- A point p is inside the triangle defined by 𝑎, b, c if and only if \[ 0 < \alpha < 1 , \quad 0 < \beta < 1 , \quad 0 < \gamma < 1 . \] This property provides an easy way to test if a point is inside a triangle.
- If one of the barycentric coordinates is 0 and the other two are between 0 and 1, the corresponding point p is on one of the edges of the triangle.
- If any barycentric coordinate is less than zero, then p must lie outside of the triangle.
- If two of the barycentric coordinates are zero and the third is 1, the point p is at one of the vertices of the triangle.
- By changing the values of α, β, γ between 0 and 1, the point p will move smoothly inside the triangle. This can (and will) be applied to other properties of the vertices such as color problem.
- The center of the triangle is obtained when α = β = γ = ⅓. If the triangle is made of a certain substance which is evenly distributed throughout the triangle, then these values of α, β, γ would give us the center of gravity.
Let A𝑎, Ab and Ac be as in figure 1 and let A denote the area of the triangle. Also note that the point inside the triangle on figure 1 is the point we called p. Consider the triangles in the figure. These are different triangles drawn for a fixed value of β. They have the same area since they have the same base and height. This area was denoted Ab on figure 1. Thus, we see that Ab only depends on β. Therefore, we have \[ A_b = C\beta . \] for some constant C. When p is on b that is when β = 1, we have Ab = A. Hence, A = C. Therefore we see that \[ \beta = \frac{A_b}{A} . \] Similarly, we have \[ \alpha = \frac{A_a}{A} , \qquad \gamma = \frac{A_c}{A} . \] In coordinates, these parameters become \[ \beta = \frac{\begin{vmatrix} x_a - x_c & x - x_c \\ y_a - y_c & y - y_c \end{vmatrix}}{\begin{vmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{vmatrix}} , \] \[ \gamma = \frac{\begin{vmatrix} x_b - x_a & x - x_a \\ y_b - y_a & y - y_a \end{vmatrix}}{\begin{vmatrix} x_b - x_a & x_c - x_a \\ y_b - y_a & y_c - y_a \end{vmatrix}} , \]
Let us assume that we are using the RGB model. That is all colors can be obtained by mixing R (red), G (green) and B (blue). Usually, with such a model, the level of each color channel is a number between 0 and 255. To specify the color at any point, we must specify a triplet (R, G, B) where R, G, and B are integers between 0 and 255. They indicate how much of red, green and blue is used in the color. When using Java, there is a built-in class to handle colors. It is called Color. This class has some built-in predefined colors. Here are some examples: Color.black, Color.blue, Color.cyan, Color.gray, Color.green, Color.magenta, Color.orange, Color.pink, Color.red, Color,white, Color.yellow. To get any other color, one uses a statement such as new Color(R,G,B) where R,G,B are integers between 0 and 255.
It is also possible to use a single integer to represent colors. Keeping in mind that an integer has 32 bits, bits 0 − 7 contain the R level, bits 8 − 15 contain the G level and bits 16−23 contain the B level. The remaining bits are unused and set to 0. Let us see now how barycentric coordinates can be used to smoothly color a triangle, given the color of its vertices. Using the notation above, let us assume that C𝑎 is the color of 𝑎, Cb is the color of b and Cc is the color of c. Each color is in fact a triplet. We will use the notation C𝑎 = (R𝑎, G𝑎, B𝑎) and similar notation for the remaining points. We would like to color the triangle so that there is a smooth coloring throughout the triangle. We use the fact that by changing the values of α, β, γ between 0 and 1, the point p = α𝑎 + βb + γc will move smoothly inside the triangle. In other words, small changes in α, β, γ will result in small changes in the location of p. We apply this to colors. We let \[ C = \alpha C_a + \beta C_b + \gamma C_c \] (we really do this for every color channel). Small changes in α, β, γ will result in small changes in the color. Therefore, the color will change smoothly as we move within the triangle. To color smoothly a triangle given the color of its vertices, we can use the following algorithm:
- For each point P = (x, y) inside the triangle, find α, β, γ.
- Use α, β, γ to interpolate the color of the point from the color of the vertices using relation \[ C = \alpha C_a + \beta C_b + \gamma C_c \]
- Plot the point with coordinates (x, y) and color computed above.
3D case:
We use the same notation as in the 2D case. The only difference is that now points have three coordinates. So, we have 𝑎 = (x𝑎, y𝑎, z𝑎), b = (xb, yb, zb) and c = (xc, yc, zc). Barycentric coordinates are extended naturally to 3D triangles and they have the same properties. In other words, we have the same equation for point p = α𝑎 + βb + γc.
The only difference of 3D compared to 2D is that the area of the triangle is alwuas positive independently on orientation. We define the following quantities:
- n is the normal to the triangle T with vertices (𝑎, b, c) in counterclockwise order. In other words, n = (b − 𝑎) × (c − 𝑎).
- n𝑎 is the normal to T𝑎, the triangle with area A𝑎 as shown in figure 1. T𝑎 = (b, c, p) in counterclockwise order. Thus, n𝑎 = (c − b) × (p − b).
- nb is the normal to Tb, the triangle with area Ab as shown in figure 1. Tb = (c, 𝑎, p) in counterclockwise order. Thus, nb = (𝑎 − c) × (p − c).
- nc is the normal to Tc, the triangle with area Ac as shown in figure 1. Tc = (𝑎, b, p) in counterclockwise order. Thus, nc = (b − 𝑎) × (p − 𝑎).
Dot product in floating point format
All arithmetic operations performed by computers over floating point numbers are subject to round-off procedure, which is a mapping of real numbers into floating-point numbers. Let fl(x) denote the rounding-off result for x. For instance, fl(π) = 0.31415926 × 10−1. Then
The dot product of two vectors, when calculated with floating-point numbers, can be affected by rounding errors. This is because floating-point arithmetic involves approximations, and repeated multiplication and addition can lead to accumulated errors, especially when dealing with very large or very small numbers (Avogadro's number = 6.023 x 1023 and Planck's constant = 6.626068 x 10-34).
Since x • y does not necessarily have a representation in the floating-point format with bounded mantissa, there is no algorithm which always computes dot-products exactly. Thus, one seeks to construct an algorithm which computes a floating-point number with minimal deviation from the exact result where the deviation should not depend on the number of addends.
Although floating point error analysis done in numerical linear algebra, we consider a simple algorithm for evaluation of the dot product of two vectors x • y:
s = 0;
for i = 1:n
s = s + x(i)∗y(i);
end
At the first step, we have
Now we apply the triangle inequality (and |δi|, |ϵi| ≤ η) to the difference between the computed and exact values:
We consider two numerical vectors with entries from ℚ4: \[ \mathbf{a} = \left( \frac{3}{7} , \ \frac{2}{5},\ \frac{6}{13} , \ \frac{11}{23} \right) , \quad \mathbf{b} = \left( \frac{7}{15} , \ \frac{5}{12} , \ \frac{23}{47} , \ \frac{5}{11} \right) . \] Their dot product in exact arithmetics is \[ \mathbf{a} \bullet \mathbf{b} = \frac{3481}{4230} \approx 0.8229314420803783 . \]
- Find the dot product of the following pairs of vectors. \[ {\bf (a)\ \ } \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix} , \quad \begin{pmatrix} 8 \\ 6 \\ 1 \end{pmatrix} \qquad {\bf (b)\ \ } \begin{pmatrix} 3 \\ 5 \\ 6 \end{pmatrix} , \quad \begin{pmatrix} -9 \\ 2 \\ 3 \end{pmatrix} \]
- how that for any vectors, x, y ∈ ℝn, we have \[ \| \mathbf{x} + \mathbf{y} \|^2 = \| \mathbf{x} \|^2 + 2\,\mathbf{x} \bullet \mathbf{y} + \| \mathbf{y} \|^2 . \]
- For vectors u, v ∈ ℝn, show that \( \displaystyle \quad (\mathbf{u} \bullet \mathbf{v}) = \frac{1}{4} \left( \| \mathbf{u} + \mathbf{v} \|^2 - \| \mathbf{u} - \mathbf{v} \|^2 \right) . \)
- Prove the parallelogram identity: \[ \| \mathbf{u} + \mathbf{v} \|^2 + \| \mathbf{u} - \mathbf{v} \|^2 = 2\, \| \mathbf{u} \|^2 + 2\,\| \mathbf{v} \|^2 . \]
- What is the angle between the vectors i + j and i + 3j?
- What is the area of the quadrilateral with vertices at (1, 1), (4, 2), (3, 7) and (2, 3)?
- Find cos(θ) where θ is the angle between the vectors \[ \left( 3, -2, 7 \right) \quad \mbox{and} \quad \left( 5,3,4 \right) . \]
- Find cos(θ) where θ is the angle between the vectors \[ \left( \right) \quad \mbox{and} \quad \left( \right) . \]
- Verify the Cauchy inequality for vectors \[ \left( \right) \quad \mbox{and} \quad \left( \right) . \]
- Find proju(v) where \[ \left( \right) \quad \mbox{and} \quad \left( \right) . \]
- Find proju(v) where \[ \left( \right) \quad \mbox{and} \quad \left( \right) . \]
- Decompose the vector v into v = v∥ + v⊥, where \[ \left( \right) \quad \mbox{and} \quad \left( \right) . \]
- Show that \[ \mathbf{u} \bullet \left( \mathbf{v} - \mbox{proj}_u (\mathbf{v}) \right) = 0 \] and conclude every vector in &Ropf'n can be written as the sum of two vectors, one of which is orthogonal and another is parallel to the given vector.
- Are the vectors u = (2, 3, −1, 4) and v = (?, ?, ?, ?) T orthogonal?
- Aldaz, J. M.; Barza, S.; Fujii, M.; Moslehian, M. S. (2015), "Advances in Operator Cauchy—Schwarz inequalities and their reverses", Annals of Functional Analysis, 6 (3): 275–295, doi:10.15352/afa/06-3-20
- Bunyakovsky, Viktor (1859), "Sur quelques inequalities concernant les intégrales aux différences finies" (PDF), Mem. Acad. Sci. St. Petersbourg, 7 (1): 6
- Cauchy, A.-L. (1821), "Sur les formules qui résultent de l'emploie du signe et sur > ou <, et sur les moyennes entre plusieurs quantités", Cours d'Analyse, 1er Partie: Analyse Algébrique 1821; OEuvres Ser.2 III 373-377
- Deay, T. and Manogue, C.A., he Geometry of the Dot and Cross Products, Journal of Online Mathematics and Its Applications 6.
- Gibbs, J.W. and Wilson, E.B., Vector Analysis: A Text-Book for the Use of Students of Mathematics & Physics: Founded Upon the Lectures of J. W. Gibbs, Nabu Press, 2010.
- Magnus, J. R. (1988). Linear Structures. Charles Griffin, London.
- Marcus, M. & Minc, H. (1992). A Survey of Matrix Theory and Matrix Inequalities. Dover Publications. Corrected reprint of the 1969 edition.
- Schwarz, H. A. (1888), "Über ein Flächen kleinsten Flächeninhalts betreffendes Problem der Variationsrechnung" (PDF), Acta Societatis Scientiarum Fennicae, XV: 318, archived (PDF) from the original on 2022-10-09
- Solomentsev, E. D. (2001) [1994], "Cauchy inequality", Encyclopedia of Mathematics, EMS Press
- Steele, J. M. (2004). The Cauchy–Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press.
- Vector addition

